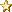For eksempel at økt antiskate tvinger armen mer innover, og at høyre kanal er på indre siden av rillen.
Dett er et annet spørsmål som besvares feil,,
Etter en lengre krangel hvor jeg har avvist 2-3 forslag til kommer vi til enighet med dette svaret:
Assumptions and Definitions
- Let:
• m₍cart₎ = cartridge mass
• m₍cw₎ = counterweight mass
• L = effective arm length (distance from the pivot to the stylus)
• r₀ = original distance of the counterweight from the pivot
Step 1. Balancing the Added Cartridge
When you add a cartridge at the tip, it produces an extra "moment" or torque equal to:
m₍cart₎ × L
To balance that extra moment, you slide the counterweight outward (away from the pivot) by a distance we'll call δ (delta). The extra moment supplied by moving the counterweight is approximately:
m₍cw₎ × δ
For balance, set these equal:
m₍cart₎ × L = m₍cw₎ × δ
Thus, the distance you must move the counterweight outward is:
δ = (m₍cart₎ × L) / m₍cw₎
Step 2. Change in the Counterweight’s Moment of Inertia
The moment of inertia of a mass is given by its mass times the square of its distance from the pivot.
- Initially, the counterweight’s moment of inertia is:
I₍cw,orig₎ = m₍cw₎ × (r₀)²
- After moving outward by δ, its new distance from the pivot becomes (r₀ + δ) and the new moment of inertia is:
I₍cw,new₎ = m₍cw₎ × (r₀ + δ)²
The change in the counterweight’s moment of inertia is:
ΔI₍cw₎ = I₍cw,new₎ – I₍cw,orig₎
= m₍cw₎ × [(r₀ + δ)² – (r₀)²]
Expanding the square:
(r₀ + δ)² = r₀² + 2 × r₀ × δ + δ²
So,
(r₀ + δ)² – r₀² = 2 × r₀ × δ + δ²
Thus,
ΔI₍cw₎ = m₍cw₎ × (2 × r₀ × δ + δ²)
Step 3. Converting the Change in Inertia to “Effective Mass”
The effective mass (m₍eff₎) is defined as the moment of inertia divided by L². That is, any extra inertia ΔI shows up as extra effective mass Δm by:
Δm = ΔI / L²
So the extra effective mass from moving the counterweight is:
Δm₍cw₎ = [m₍cw₎ × (2 × r₀ × δ + δ²)] / L²
Remember, the cartridge itself contributes directly its mass (m₍cart₎), because it is at the end (distance L) so its moment is m₍cart₎ × L² and dividing by L² gives m₍cart₎.
Therefore, the
net change in effective mass is:
Δm₍eff₎ = m₍cart₎ + Δm₍cw₎
= m₍cart₎ + [m₍cw₎ × (2 × r₀ × δ + δ²)] / L²
Step 4. Substitute for δ
We already found that:
δ = (m₍cart₎ × L) / m₍cw₎
Substitute this into the extra inertia term:
- First, compute 2 × r₀ × δ:
2 × r₀ × δ = 2 × r₀ × (m₍cart₎ × L / m₍cw₎) = (2 × r₀ × m₍cart₎ × L) / m₍cw₎
- Next, compute δ²:
δ² = (m₍cart₎ × L / m₍cw₎)² = (m₍cart₎² × L²) / m₍cw₎²
Now, plug these back in:
Δm₍cw₎ = [m₍cw₎ × ((2 × r₀ × m₍cart₎ × L) / m₍cw₎ + (m₍cart₎² × L²) / m₍cw₎²)] / L²
Cancel m₍cw₎ in the first term:
= [2 × r₀ × m₍cart₎ × L + (m₍cart₎² × L²) / m₍cw₎] / L²
= (2 × r₀ × m₍cart₎ × L) / L² + (m₍cart₎² × L²) / (m₍cw₎ × L²)
= (2 × r₀ × m₍cart₎) / L + m₍cart₎² / m₍cw₎
So, the net effective mass change becomes:
Δm₍eff₎ = m₍cart₎ + (2 × r₀ × m₍cart₎) / L + m₍cart₎² / m₍cw₎
Thus, the new effective mass of the system is:
m₍eff,new₎ = m₍eff,old₎ + Δm₍eff₎
= m₍eff,old₎ + m₍cart₎ + (2 × r₀ × m₍cart₎) / L + m₍cart₎² / m₍cw₎
In Plain English
- Adding the Cartridge:
Placing a cartridge at the end of the tonearm appears to add its mass (m₍cart₎) to the effective mass.
- Rebalancing the Tonearm:
To balance the extra torque, you must slide the counterweight outward by δ = (m₍cart₎ × L) / m₍cw₎.
- Extra Inertia from the Counterweight:
Moving the counterweight outward increases its distance from the pivot. Since inertia depends on the square of the distance (r²), this move adds extra "inertia" equivalent to:
(2 × r₀ × m₍cart₎) / L plus a small term m₍cart₎² / m₍cw₎.
- Total Change:
The overall effective mass increases by the cartridge mass plus these extra contributions from moving the counterweight.
Let's recalculate with the following parameters:
- Effective arm length, L: 230 mm
- Initial effective mass: 10 g
- Counterweight mass, m₍cw₎: 100 g
- Cartridge mass, m₍cart₎: 8 g
- Counterweight's original distance from the pivot, r₀: 21 mm
1. Determine the Counterweight Shift (δ)
When you add the cartridge at the tip, its extra moment (8 g × 230 mm) must be balanced by moving the counterweight outward. The distance the counterweight is shifted is given by:
δ = (m₍cart₎ × L) / m₍cw₎
Plug in the numbers:
δ = (8 × 230) / 100
= 1840 / 100
=
18.4 mm
This distance does not depend on r₀; it remains 18.4 mm.
2. Calculate the Extra Effective Mass from Moving the Counterweight
When the counterweight is moved outward, its contribution to the moment of inertia increases. The extra effective mass from this move is given by:
Δm₍cw₎ = (2 × r₀ × m₍cart₎) / L + (m₍cart₎²) / m₍cw₎
First term:
(2 × r₀ × m₍cart₎) / L = (2 × 21 × 8) / 230
= (336) / 230
≈ 1.46 g
Second term:
(m₍cart₎²) / m₍cw₎ = (8²) / 100 = 64 / 100 = 0.64 g
So, the extra effective mass from shifting is:
Δm₍cw₎ ≈ 1.46 g + 0.64 g =
2.10 g
3. Determine the Net Increase in Effective Mass and the Final Value
Direct contribution from the cartridge:
Since the cartridge is at the end (distance L), it adds its own mass, i.e., 8 g.
Total net increase:
Δm₍eff₎ = m₍cart₎ + Δm₍cw₎
= 8 g + 2.10 g
=
10.10 g
Now, adding this to the initial effective mass:
m₍eff,new₎ = m₍eff,old₎ + Δm₍eff₎
= 10 g + 10.10 g
≈
20.1 g
som er det jeg regnet ut selv først før jeg spurte AI
For min følelse etter denne siste justeringen etter å ha byttet til nyere generasjon armbrett ble betydelig bedre enn de tidligere forsøkene mine på justering iallefall. Så får ting utvikle seg videre i takt med at jeg opparbeider meg mer erfaring med spilleren. Venstre side ser ut til å være bra i flukt med plinthet både ved syn og banking.
Men en ting er jo klart, man kan jo bytte en god del ting før man når opp i prisen av en tilsvarende ny da, selv om en ny da er perfekt og ikke helt sammenlignbar pga at alt er modernisert...om ikke annet er det positive med å starte med en slik gammel en at man lærer både mye om historien og den generelle oppbyggingen av spilleren...
