TPA3255

[duc916]

Klotz mikrofonkabel.

https://www.speakon.no/klotz-mc2000-profesjonell-mic-kabel-sort.html

De har en standardversjon også, den er noen få kr billigere.

 

[Pær]

Denne? Ser fin ut. Bruker du en av inner-lederne og skjermingen eller bare inner-lederne?

Original Japan Mogami 2791 Dual Core Audio Cable Pure Copper Braided Shielding Net Cold and Heat Resistant Outdoor Use Super - AliExpress 44

Smarter Shopping, Better Living! Aliexpress.com

m.aliexpress.com

Ja den ja.
Har brukt den med litt forskjellig kobling. Brukt den med bare lederne(signal + jord), eller begge leder (signal R og L) og skjerming (Jord). Har også satt den opp med en leder (signal) + en leder som er koblet til skjem i ene enden (jord). Kort fortalt, den er veldig fleksibel og anvendelig.
Et eksempel:

 

[Dalemark]

Ja den ja.
Har brukt den med litt forskjellig kobling. Brukt den med bare lederne(signal + jord), eller begge leder (signal R og L) og skjerming (Jord). Har også satt den opp med en leder (signal) + en leder som er koblet til skjem i ene enden (jord). Kort fortalt, den er veldig fleksibel og anvendelig.
Et eksempel: Vis vedlegget 1171387

Supert. Prøver denne.

 

[Dalemark]

Da er endelig input bufferet kommet fra jlcpcb. Har tatt en del tid å designe da dette er helt nytt territorium for meg. Det er nok ikke optimalt plass utnyttet. Ble litt stort og rotete når jeg skulle route det.
Jeg hadde volt regulator og inlet liggende men fikk jlc til å montert resten.

Uttak av buffer blir nesten liggende imot en kondensator på ampen og jeg sliter litt med å få flyttet disse til en mer passende plass.

 

[Armand]

Har du testet om det virker?
Ikke at du spurte, men jeg ser dessverre en del feil

Her ser det ut som + og - inngangen er koblet sammen. Det kan de ikke være.

Spenningen inn til regulatoren går gjennom kondensator C3. Denne må til GND.

Er det GND her?

Du har ingen avkoblingskondensatorer på opampene. Dette kan gå bra, men fører ofte til oscilleringer. Man bør som minimum ha 100nF helt inntil hver opamp per railspenning.

Det ser ut som koblingskondensatorene på utgangene (C7-C14) er MLCC med dielektrikum av X7R eller lignende. Disse forvrenger lyden ganske mye.

Inngangsmotstandene er 1k. Det er svært lavt.
RF kondensatorene på 100pF burde sitte helt inntil inngangene og ha retur kortest mulig vei til GND. Når disse er spredt utover kortet uten kort retur til GND (og chassis) vil RF kommer inn på kortet ditt.

Beklager å komme med mange dårlige meldinger, men jeg ville kikket litt nærmere på disse tingene.

 

[Dalemark]

Har sett på det.

Ja, her var jo litt av hvert. Jeg på tynn is og innehar ikke kunnskapen som trengs. Forsøker å skjønne sammenhengen dels ved å se på andre løsninger og dels ved å studere datablad på komponentenen og så får jeg litt tips på DIY Audio. Jeg har tenkt å bruke +4dBu som gain på Fireface UCX som gir 1,228 Volt . Texas Instruments opgir TPA3255EVM til 21,5dB i SE mode.

R25 på bufferet blir da som følger:
R25=2*2,2(R17,R16)/(A-1)
A=(9,206/1,228)-1
A=6,496
R25=2*2,2/A=677 Ohm

Jeg velger R25=560 Ohm

Ikke bra med pluss og minus sammen. Har helt overset dette. Forbasket.
Rettet spenningen inn i regulator og kondensator C3 til jord. Jeg antok det var GND ved mounting hullet, men jeg har ingen GND krets til hullet. Byttet inngangsmotstandene til 30k Ohm. Avkoblingskondensatorer er lagt til men jeg er usikker på antallet. Trenger jeg 4 stk. pr dual opamp eller bruker jeg 2?
Hvilke kondensator type vil du anbefale som koblings kondensator på utgangene?
Dersom Schematic blir ok skal jeg legge ut komponentliste.

Det er bare fint med tilbakemeldinger. Det er jo det man lærer av.

 

[Armand]

Du har satt 100nF kondensatorer på alle opamp inngangene. Dette er ikke avkobling.
Jeg ønsker jo ikke å ødelegge for deg, men for å være brutalt ærlig: Du er ganske langt unna den forståelsen man trenger for å lage et buffer som er bra.
F.eks så er layout på kortet ditt helt feil. Det er lange baner på kryss og tvers over et stort område og det er ingen tanke for hvordan strømmene og signalene skal gå på kortet ditt.
Det spiller stor rolle hvor tykke banene er, og hvor komponentene sitter, hva de gjør, type komponenter, antall lag på kortet osv osv.
Min anbefaling er:
1. Simuler kretsene dine
2. Se på eksempler på hvordan andre har laget sine design og forstå hvorfor. Det er mange som har lagt ut PCB design på DIY audio.
3. Se på videoer.
Eric Bogatin kan "alt"

4. Se på eksempler fra hvordan de som lager opamper gjør det.

https://www.ti.com/lit/ug/snaa052a/snaa052a.pdf?ts=1769680471254&ref_url=https%253A%252F%252Fwww.ti.com%252Fsitesearch%252Fen-us%252Fdocs%252Funiversalsearch.tsp%253FlangPref%253Den-US%2526nr%253D5505%2526searchTerm%253Dheadphone+amplifier

 

[Pær]

Gøy å følge med @Dalemark , liker innstillingen Er ingen ekspert, men det jeg har forstått er at det anbefales en MLCC 100nf så nært så mulig på Vs- og Vs+. Arrester meg gjerne om det er feil.

 

[Armand]

Gøy å følge med @Dalemark , liker innstillingen Er ingen ekspert, men det jeg har forstått er at det anbefales en MLCC 100nf så nært så mulig på Vs- og Vs+. Arrester meg gjerne om det er feil.

Det stemmer det, men det er like viktig at de er koblet til et lavimpedant jordplan og at ikke returstrømmer i jordplanet modulerer jord.
Jord er ikke bare jord. I audikretsløp er dette kritisk og ikke helt rett frem å få korrekt. Bland så sikkerhetsjord til strømnettet inn i miksen og man har en del ting som må gjøres korrekt skal man unngå støy, brum og RF-støy.

 

[Dalemark]

Takk for tilbakemelding @Armand . Fint at du er ærlig.

Foreløpig utkast av ny versjon er basert på mye tid med youtube videoer av andre løsninger og teori forståelser.

Jeg synes dette er morsomt. Dersom det viser seg at resultatet vil fungere blir det årets store julepresang til meg selv og dem er det langt mellom for en gammel utdanket sveiser.

Dette bufferet vil jeg lodde selv. Jeg har liggende flesteparten av komponentene da jeg handlet inn flere av samme for et balanserte bufferkortet. Det er et stereobrett og JLCPCB har minimumsordre på 5 brett. Her har jeg brukt kortere og tykkere baner. Har jord på topp og bunnlag. Jeg forsøker og separere inntak til regulatorene med tanke på RF støy. Er usikker på plassering av utgangsregulator LM337. Skulle denne kanskje stått på kanten av kortet? Det har vært litt utfordring og route denne. Designe sjekk (DRC) viser ok men jeg må lære meg å simulere kretsene.

Håper på innspill.

 

[KJ]

Takk for tilbakemelding @Armand . Fint at du er ærlig.

Foreløpig utkast av ny versjon er basert på mye tid med youtube videoer av andre løsninger og teori forståelser.

Jeg synes dette er morsomt. Dersom det viser seg at resultatet vil fungere blir det årets store julepresang til meg selv og dem er det langt mellom for en gammel utdanket sveiser.

Dette bufferet vil jeg lodde selv. Jeg har liggende flesteparten av komponentene da jeg handlet inn flere av samme for et balanserte bufferkortet. Det er et stereobrett og JLCPCB har minimumsordre på 5 brett. Her har jeg brukt kortere og tykkere baner. Har jord på topp og bunnlag. Jeg forsøker og separere inntak til regulatorene med tanke på RF støy. Er usikker på plassering av utgangsregulator LM337. Skulle denne kanskje stått på kanten av kortet? Det har vært litt utfordring og route denne. Designe sjekk (DRC) viser ok men jeg må lære meg å simulere kretsene.

Vis vedlegget 1178400



Vis vedlegget 1178401

Vis vedlegget 1178403

Vis vedlegget 1178404

Håper på innspill.

Du har positiv tilbakekobling på et par opamper. Deter kanskje ikke meningen?

Edit + hva er hensikten med H1?

Mvh
KJ

 

[Armand]

Dette er mye bedre
Men vi er jo ikke mål. Du må simulere.
Tina-TI er et gratis og veldig kraftig verktøy. Registrer deg og last ned.

TINA-TI Simulation tool | TI.com

View the TI TINA-TI Simulation tool downloads, description, features and supporting documentation and start designing.

www.ti.com

Pakk så ut den vedlagt zip-filen og åpne filen.
Trykk på CTRL+ALT+Aog du får opp gain-plottet som på bildet under. (I menyen er det Analysis -> AC Analysis -> AC Transfer Analysis)

Som du ser så gir kretsen din et gain på 18,36dB. Det er nok litt høyt. Det er R3 som bestemmer gain. Endre på denne og prøv deg frem.

Vil du simulere balansert inn, kobler du slik:

Du vil få samme gain.

Dobbeltklikk på Source og trykk på de tre prikkene ved Sine Wave og velg spenning og frekvens. (Her 6,7V og 1kHz)

Trykk CTRL+ALT+T (iI menyen: Analysis -> Transient)
Velg tiden du vil se på

Vi ser at det klipper så det ljomer.


Hvis du gjør dette så vil du se at det er et par feil i skjema ditt. Opamper feil vei (speilvendt) og feil motstandsverdier.

 

[Armand]

Det fine med Tina-TI er at nå simulerer vi med akkurat den opampen du skal bruke, og man kan se på støy og andre ting også.
Man kan også se på hva som skjer med single ended og balansert input, hvordan det påvirker CMRR og mye annet. Men det kan man ta etterhvert.
Når det gjelder layout, ser det jo MYE bedre ut nå
Jeg har ikke kikket så nøye på det, men det er en del feil.
100nF avkoblingskondensatorene heter R8 -R11?? De er heller ikke plassert inntil opampene.
-5V går til pinne 8 som er pluss
C10 og C13 har polaritet feil vei.

Vurder å bruke 4-lags kort. Det koster nesten ingenting ekstra og gir mye bedre muligheter til å sikre et 100% jordplan selv om det ser bra ut nå.

 

[Dalemark]

100nF avkoblingskondensatorene heter R8 -R11?? De er heller ikke plassert inntil opampene.
-5V går til pinne 8 som er pluss
C10 og C13 har polaritet feil vei.

Vurder å bruke 4-lags kort.

Justert dette.

Og jobbe med sinuskurven ved å bytte komponenter var optimalt . Hvorfor brukes 6.7V?

Dette er så nære jeg kommer ved og bytte på motstand R2, R3 og R4, men gain er helt nede i 3,53dB. Det er vel noe lavt. Hva er prioritert? Ser du har lagt til R11 og 12. Er dette for å kjøre det i Tina-TI?

 

[Armand]

Bra du er i gang med simulering. Bruk AI for å få tips til ting du lurer på. Du kan f.eks lime inn bilde av skjema ditt og få AI til å finne feil.
6,7V var bare tilfeldigvis en spenning fra et av mine prosjekter.
Hvilken gain du bruke er helt opp til deg og ditt utstyr. Det er ikke noen generell fasit på dette.

R11 og R12 brukes for å sikre stabiliteten til opampene når det kobles på kabler på utgangen. Disse har en eller annen kapasitans på noen hundre pF, og da vil opampene begynne å oscillere ved en svært høy frekvens på noen MHz. Dette er ikke alltid helt enkelt å måle, men fører til ulieariteter i audioområdet. Du se at "alle" kretsløp har en motstand på utgangenpå typisk 50-100 Ohm. Ingen vits å gå høyere enn 100 Ohm. Det er også vanlig å bruke en koblingskondensator på utgangen. Ingen vits å røre med med olje i gull og annet svada. Bare en vanlig 100uF bipolar funker 100%. Jeg har målt, og forvrengning er et ikke-tema.

* Sjekk polariteten på alle kondensatorene dine. Det er fremdeles mange som står feil vei.
* Noen av kondisene heter fremdeles både "R" og "U". Dette må bare fikses.
* Hvorfor er ikke GND med i power supply input kontakten og audio kontaktene?
* R3 skal være 2,2M (ikke milli).
* Du må fortelle litt om hva som er tanken bak designet ditt. Hva skal inn på CN2, CN4 og H1?

 

[Dalemark]

Bakgrunnen for designet er å justere gain input for TI3255evm. Det er kraftig mye støy i diskant og mellomtonehornene. En løsning som også inkluderte dual opamp virket interessant. Har alltid likt å finne ut av hvordan ting fungerer. Så hvorfor ikke hoppe ut i dette.

Jeg bruker 3255 som 4 kanaler og må dermed ha 2 buffer kort. CN2 og CN4 er høyre og venstre kanal.

Plan for H1 er å kunne laske inverting audio input signal (-) fra begge kanalene slik at det blir likt TI3255evm oppsettet i SE mode. Jeg er usikker på om dette blir rett.

Hvorfor er ikke GND med i power supply input kontakten og audio kontaktene?

Er det felles GND på audio inn du mener? I så fall kan jeg droppe H1. Min konfigurasjon justerer gain, men vanligvis brukes vel 1 stk. dual opamp for 2 kanaler hvor inverting A og B input blir V og H side. Altså stereo.

Jeg vil forsøke å få til en switch til pin7 og pin8 på dip8 socket da tanken er å kunne forsøke Burson opampV6 vivid som jeg har liggende. Disse har en socket hvor P7/P8 bytter plass.

 

[cbarth1]

Må bare si at disse 3255 forsterkerne imponerer. Kjøpte først en 3E Audio A7 stereo til tv-anlegget. Ble så imponert over denne at jeg solgte rørforsterkeren min og kjøpte A7 monoblokkene. Nå med oppgraderte opamper spiller de helt latterlig bra.

 

[Armand]

Det er fremdeles ganske uklart for meg hva du egentlig ønsker å oppnå.
Jeg har skjønt at du vil ha et buffer, men:
1. Skal det værte single ended eller balansert input?
2. Skal det være single ended eller balansert utgang?
3. Skal du kunne konfigurere det til å brokoble utgangene?
4. Skal du ha fire kanaler? I så fall, lag alle på samme PCB.

GND er en del av strømforsyningen og jeg har aldri sett noen lage et kretskort der ikke GND er en del av power input.
Man kan jo koble inn GND andre steder på kortet også, men det er liksom bare helt rart.
GND er det vanskeligste av alt når man lager audiokretsløp. Skal man optimalisere bør man vite hvor returstrømmene går og designe jordplanet ut i fra dette. I ditt tilfelle der du lager et enkelt buffer, er det å lage et enkelt stort felles jordplan det sikreste man kan gjøre.

Jeg skjønner ikke hva du mener med dette: " Plan for H1 er å kunne laske inverting audio input signal (-) fra begge kanalene slik at det blir likt TI3255evm oppsettet i SE mode. Jeg er usikker på om dette blir rett."
Link gjerne til steder du henter info fra og hva som er planen din. Det gjør det enkelre å forstå hva du vil oppnå.

 

[Dalemark]

1. Skal det værte single ended eller balansert input?
2. Skal det være single ended eller balansert utgang?
3. Skal du kunne konfigurere det til å brokoble utgangene?
4. Skal du ha fire kanaler? I så fall, lag alle på samme PCB.

1. Singel ended.
2. Singel ended.
3. Nei. Jeg skal kunne ha felles jord på inngangene og utgangenen. Mulig du kaller dette brokoble. Blir litt forvirret når du snakker om å brokoble kilde signaler.
4. Ja.

I ditt tilfelle der du lager et enkelt buffer, er det å lage et enkelt stort felles jordplan det sikreste man kan gjøre.

Dette har jeg ikke satt meg inn i ennå. Mulig jeg burde gjort det tidligere. Jeg har allerede bygget et kort som er fullstendig feil og ønsker ikke å gjøre det igjen. Derfor er dette fremdeles bare foreløpig. Jeg vurderte å bruke en av disse til schassis jord.

Kortet er basert på dette, vel å merke balanserte 1kanal kortet som dermed kanskje ikke har så store jordutfordringer.

Felles jord:

 

[Armand]

Den kretsen du har sett på er for balansert audio. Siden du skal ha SE inn og SE ut er det ingen vits å lage den.
Du skal drive alle fire kanalene på et TPA3255EVM kort skriver du. Det er dette kortet?

TPA3255EVM Evaluation board | TI.com

View the TI TPA3255EVM Evaluation board description, features, development resources and supporting documentation and start designing.

www.ti.com

Her er skjema for dette kortet:

https://www.ti.com/lit/df/slar129a/slar129a.pdf?ts=1770801062931

Her er bruksanvisningen:

https://www.ti.com/lit/ug/slou441/slou441.pdf?ts=1770833035183&ref_url=https%253A%252F%252Fwww.ti.com%252Ftool%252FTPA3255EVM

I bruksanvisningen står det at kortet er laget for å ta i mot 2V RMS, og det kan konfigureres til alt fra 1 til 4 kanaler.

Her ser du at det allerede sitter et buffer på dette kortet. Signalet går rett fra input til en NE5532 opamp. Denne opampen er mer enn god nok til å matche ytelsen til TPA3255 som har mange ganger høyere både støy og forvrengning av alle typer enn NE5532.

Å lage et buffer før denne bufferen gir for meg ingen mening. I hvert fall ikke hvis bufferet skal baseres på en ultra lav støy/THD opamp som OPA1642.

 

[cbarth1]

3E Audio A7 inklusive 48V / 10A strømforsyning koster 315 euro pluss moms og frakt. Klarer man å bygge noe bedre til den prisen? Den har selvsagt PFFB som virkelig har tatt disse 3255 forsterkerne til ett nytt nivå.

3E AUDIO A7 Amplifier

3E Audio, a recognized player in the DIY world, now offers a Class D Stereo amplifier incorporating audiophile Hi-Fi components. The A7 amplifier is based on two TI TPA3255 chips in PBTL configuration, and two dual OPA1612A OPAs.

www.audiophonics.fr

 

[Armand]

Denne visste jeg ikke om. At du for prisen til et par vinterdekk kan få en forsterker som yter så bra er jo hinsides.

På småsignalnivå (5W) som er typisk for vanlig lytting på moderate nivå er den like god som forsterkere i 40k++ klassen

Den klarer faktisk å levere over 200W i 4 Ohm kontinuerlig! Jeg testet Fosi sin monoversjon jeg kjøpte i fjor, og den brant opp under samme test

 

[cbarth1]

Har denne som sagt både i stereo og mono versjon. Har hatt ganske mye spennende innom racket, og disse står ikke tilbake for noen av dem i mine ører. Dette er selvsagt min subjektive oppfatning. Men smaken er som baken, disse kler min musikksmak.

 

[Hornlyd]

PS! TPA3255EVM som kan drives som 4/2/1 kanal har svært lav gain som 4 kanal. Har testet.

Som nevnt tidligere låter den meget bra og i «standardmodus» som 2 kanal er den kraftig og dynamisk med ca 48V psu. Den var ikke vesentlig dårligere enn LM Audio 805 rørforsterker men ved lengre og mer fokusert lytting er det selvfølgelig forskjell. @Ludo har nå fått seg en MI 10 watt klasse A og rapporterer at det er litt luftigere og mer oppløst. Har ikke fått hørt det selv.

Men summarum er TPA3255EVM et kanonbra DIY objekt. Bang for the bucks.

 

[Hornlyd]

3E Audio A7 inklusive 48V / 10A strømforsyning koster 315 euro pluss moms og frakt. Klarer man å bygge noe bedre til den prisen? Den har selvsagt PFFB som virkelig har tatt disse 3255 forsterkerne til ett nytt nivå.

3E AUDIO A7 Amplifier

3E Audio, a recognized player in the DIY world, now offers a Class D Stereo amplifier incorporating audiophile Hi-Fi components. The A7 amplifier is based on two TI TPA3255 chips in PBTL configuration, and two dual OPA1612A OPAs.

www.audiophonics.fr

Hva er PFFB?

 

[Dalemark]

Pffb feedback modification reduserer støy med 6-7 dB på ti3255. Dette er forsøkt av medlemmer på DIY AUDIO.

 

[Flageborg]

 

[Hornlyd]

Skjønte ingenting men det låter altså bedre

Hvor plasserer den seg lydmessig? Blandt Anaveiw AMS0100, rimelig ICE etc?

 

[Armand]

Skjønte ingenting men det låter altså bedre

Det er ekstra feedback.
Altså at en rask opamp sammenligner signalet inn fra kilden og det som kommer ut fra effektrinnet. Hvis den "oppdager" feil f.eks at spenningen akkurat nå er 1mV for høy på utgangen, så vil den redusere signalet inn til forsterkeren tilsvarende for å korrigere.
Dette reduserer både støy og forvrengning.

 

[Flageborg]

Litt mer praktisk forklaring i denne videoen....

 

[cbarth1]

Skjønte ingenting men det låter altså bedre

Hvor plasserer den seg lydmessig? Blandt Anaveiw AMS0100, rimelig ICE etc?

Fikk blod på tann etter å ha hatt A7 stereo versjonen en stund. Tenkte at det hadde skjedd veldig mye siden jeg jadde noen Rotel Icepower monoblokker på midten av 2000-tallet. Så jeg testet A7 stereo mot en Knedahl 1200 Icepower. Tenkte at dette blir bare mye mer av det samme. Men de låt veldig forskjellig. Nå kan sikkert den Icepower'en spille mye høyere, men på lavt volum var det mye mer fylde og varme i lyden fra A7. Syntes den Icepoweren var for lys iog skarp i klangen for min del. Merk at dette var i mitt oppsett med Sparkos 2590 opamper, Icepower kan sikkert fungere knall i anlegg som er litt sirompa og mørke i utgangspunktet, eller de som må ha masse effekt for å sparke liv i høyttalerne.

 

[Dalemark]

Den kretsen du har sett på er for balansert audio. Siden du skal ha SE inn og SE ut er det ingen vits å lage den.

Takk for input. Jeg har ikke spikret noe som helst ennå. Dersom du studerer TI3255EVM dokumentasjonen vil du kunne se at opampNE5532 kan deaktiveres. Det er også mulig å bruke balansert inn og SE ut i et eksternt buffer.

Dersom vi sammenligner opampNE5532 vs opamp1642 ser vi følgende.

Funksjon	NE5532 (BJT)	OPA1642 (JFET)
Inngangsstøy	~5 nV/√Hz	~5.1 nV/√Hz
THD+N (Distorsjon)	~0.0007% (typisk)	0.00005% (ultralav)
Slew Rate	9 V/µs	20 V/µs
Båndbredde (GBW)	10 MHz	11 MHz
Strømforbruk	8 mA per kanal	1.8 mA per kanal
Inngangsbiasstrøm	200 nA (høy)	2 pA (ekstremt lav)
Utgangstype	Standard	Rail-to-rail

Ved fokus på støy ser vi at opa1612 ligger lavt.

Egenskap	OPA1612 (Bipolar)	OPA1642 (JFET)
Spenningstøy	1,1 nV/√Hz (ekstremt lavt)	5,1 nV/√Hz
Forvrengning (THD+N)	0,000015 % ved 1 kHz	0,00005 % ved 1 kHz
Inngangsstrøm (Bias)	60 nA (typisk)	2 pA (ekstremt lavt)
Strømforbruk	3,6 mA per kanal	1,8 mA per kanal
Utgangstype	Rail-to-rail	Rail-to-rail

RME 400 fireface UFX, som er kilden min, har utgansimpedanse på 75 Ohm og 30 Ohm på utgang 7/8. Dersom vi oppsumerer AI kommer følgende:

Opamp	Optimal seriemotstand	Styrke ved 75 Ohm load
OPA1612	75 Ohm	Svært lav forvrengning, utmerket linjæritet
NE5532	75 Ohm (eller 100 Ohm )	Ok, men forvrenger mer ved høy last

Konklusjon:

For best lydkvalitet og minst mulig refleksjon i en 75 ohm linje, bruk OPA1612 med en 75 Ohm 1% motstand rett etter opampens utgang (før eventuell koblingskondensator). Hvis du bruker NE5532 og opplever forvrengning, bør du vurdere å bruke en buffer etter opampen eller bytte til en sterkere opamp som OPA1612 eller OPA1622.

At valg av opamp har så stor innvirkning er kanskje tvilsomt. Jeg har nevnt tidligere at jeg synes dette er morsomt å lærerikt å holde på med og er ennå ikke i mål på hvordan man kan redusere støyen i TI3255EVM.

 

[Armand]

Slik jeg har forstått deg, ønsker du å se på om du kan senke støyen du opplever ved å lage et bedre buffer. AI forteller deg at dette er mulig ved å bruke en bedre opamp. Det svaret du har fått av AI er ikke direkte feil, men det er nyanser rundt problemstillingen som mangler.

Ja, en OPA1612 kan drive en mye tyngre last enn NE5532 med mindre forvrengning og støy, men du har rett i å mistenke at effekten er tvilsom. Det er nemlig ikke slik at en TPA3255 er krevende å drive. Faktisk er det en veldig lett last på 20k, og buffer er egentlig ikke nødvendig.

Du kan like godt koble lydkortet ditt rett inn på modulen uten å bruke bufferet

NE5532 er en svært god opamp som driver audiosignalene i millioner av kretsløp i studioer og audiokretsløp av høy kvalitet i hele verden. Den er derfor også billig i forhold til ytelsen, og et logisk valg når pris er en faktor.
Både støy og forvrengning er så lav at det er kun den aller råeste forsterkeren fra Purifi som kan få en målbar forbedring av noe bedre.
I andre sammenhenger der signalspenningen er svært lav vil også NE5532 fort være en begrensning (f.eks. RIIA, og mikrofonforsterker).

Forvrengningnen til NE5532 er slik:

Så lenge lasten er lettere enn 3k ligger den på under 0,0008% helt opp til 20kHz. I praksis er det egentlig 0,0004% siden vi ikke hører over 20kHz, og når man passerer 10kHz så ligger nærmeste forvrengning (2 harmonisk) på 20kHz.

Det er en stor sammenligning og målinger av opamper utført av professoren selv - Douglas Self - her:

Modern Op-Amp Distortion Tests: Part 1 - BJT-Input Devices

Douglas Self has been using a tried-and-true palette of op-amps in his designs. Because many new types have appeared in the last decade, he thought it was high time to evaluate those for distortion performance. In Part 1 of this article, he examines BJT-input devices using a similar protocol for...

audioxpress.com

Modern Op-Amp Distortion Tests: Part 2 — A Few More BJT Types and JFET Devices

Many new op-amp types have appeared in the last decade, and Douglas Self thought it was time to evaluate those for distortion performance. In Part 1 of his article, he measured BJT-input devices using a similar protocol for five different loads and testing for basic op-amp distortion in...

audioxpress.com

Du burde kikke på bøkene hans. De er gode og er skrevet for at menigmann skal kunne lese og forstå kretsene. Det er mange eksempler i bøkene.

En kuriositet er at hvis du napper ut NE5532 fra kortet ditt og lodder inn en OPA1612, så vil du få mer støy! Dette er fordi motstandene på 10k kommer inn i bildet og du må ta med strømstøyen fra opampen i beregningene.

Når din TPA3255 støyer så er det fordi det er den som støyer. Dette kan du enkelt sjekke ved å kortslutte inngangene (etter NE5532). Da simulerer du i praksis et "umulig" perfekt buffer.

Når man skal ha hjelp av AI hjelper det å laste opp datablader og bilder og være streng og tydelig. (Jeg lastet opp bildet av forvrengningen til NE5532, skjema av bufferet på EVM kortet og alle 3 databladene)
F.eks slik. Prompt:

Les alle databladene og analyser bildene jeg har lastet opp. Ikke lat som du vet dette selv. Du skal kun bruke data fra databladene og bildenene i dine svar, vurderinger og beregninger. Hvis det er noe du lurer på så spør du meg om svar.
Jeg har en forsterker av typen TPA3255. Det er TI's egenutviklede TPA3255EVM modul så vi kan se bort i fra at de har gjort noe dumt, og vi kan derfor ta utgangspunkt i støy og forvrengningsdata oppgitt i databladet jeg har gitt deg.
På dette kortet har TI brukt opampen NE5523 som buffer. Det er koblet som på bildet jeg har lastet opp til deg, og vi ser at gain er -1. Vis at du forstår kretsen og forklar hvorfor gain er -1.
Jeg vil at du forklarer hvor mye lavere støy vil kunne bli på utgangen av TPA3255 forsterkeren hvis jeg bytter ut NE5532 med en OPA1612 i buffertrinnet på inngangen.
Jeg vil ha tre eksempler:
* ett som tar som utgangspunkt at jeg bruker de originale 10k motstandeneklarer å utnytte OPA1612 best mulig og at jeg skal ha samme gain.
* ett som bruker optimaliserte motstansdverdier rundt OPA1612
* ett som bruker optimaliserte motstandsverdier og gain på 12dB.

Videre vil jeg også at du vurderer forbedring av forvrengning ved å bytte ut NE5532 med OPA1612.
Jeg trenger ikke nøyaktige beregninger, men jeg vil se resultatet av delberegninger og grunner til at resultatene blir som de blir.
Jeg vil ha svaret uten avanserte formeteringer i latex slik at jeg kan dele de på et forum.

Spoiler: Gemini PRO

Her er en analyse av kretsen og beregninger for støy og forvrengning basert utelukkende på de opplastede dokumentene: Buffer_TPA3255EVM.png, ne5532.pdf, opa1612-q1.pdf, tpa3255.pdf og THD_NE5532.png.

1. Analyse av kretsen og Gain
Basert på bildefilen Buffer_TPA3255EVM.png ser vi et utsnitt av inngangsbufferen.

• Komponenter: Vi ser operasjonsforsterkeren U6A (NE5532ADR).
• Konfigurasjon: Opampen er koblet som en inverterende forsterker. Inngangssignalet (INC-RCA) går gjennom en kondensator (C62) og en motstand (R20) til den inverterende inngangen (pinne 2).
• Motstandsverdier:
  • Inngangsmotstand ($R_{in}$): R20 = 10.0k
  • Tilbakemeldingsmotstand ($R_f$): R21 = 10.0k
• Gain-beregning:
  Formelen for spenningsforsterkning ($A_v$) i en inverterende opamp-kobling er:
  $A_v = - (R_f / R_{in})$
  Ved å sette inn verdiene fra skjemaet:
  $A_v = - (10.0k / 10.0k) = -1$

Dette bekrefter at kretsen er en buffer med unity gain (forsterkning på 1, men invertert fase).

2. Støyvurdering ved bytte til OPA1612
For å vurdere støyforbedringen må vi se på støyen som genereres av selve opampen, motstandene rundt den, og hvordan dette forholder seg til egenstøyen i selve effektforsterkeren (TPA3255).

Data fra databladene (ved 1 kHz):

• 
  NE5532: Spenningsstøy ($e_n$) = 5 nV/√Hz, Strømstøy ($i_n$) = 0.7 pA/√Hz.
  
  
  
• 
  OPA1612: Spenningsstøy ($e_n$) = 1.1 nV/√Hz, Strømstøy ($i_n$) = 1.7 pA/√Hz.
  
  
  
• 
  TPA3255: Utgangsstøy ($V_n$) = 85 µV (A-weighted). Gain i TPA3255 er typisk 21.5 dB (ca. 12 ganger forsterkning).
  +1
  

Eksempel 1: Bytte til OPA1612 med originale 10k motstander
Her beholder vi R20 og R21 på 10kohm.

I en krets med såpass store motstandsverdier er det termisk støy (Johnson-støy) fra motstandene som dominerer, ikke selve opampen. Termisk støy for en 10k motstand er ca. 12.8 nV/√Hz ved romtemperatur.

• Total støy ut fra bufferen vil domineres av motstandene uansett hvilken opamp du velger.
• Forskjellen mellom NE5532 (5 nV/√Hz) og OPA1612 (1.1 nV/√Hz) drukner i støyen fra 10k-motstandene.
• Resultat: Du vil få ubetydelig/ingen hørbar forskjell i støy på utgangen.

Eksempel 2: OPA1612 med optimaliserte motstander (Gain -1)
OPA1612 tåler lavere motstandsverdier godt. For å utnytte den lave støyen i OPA1612, må vi senke motstandsverdiene slik at termisk støy blir lavere enn opampens egenstøy. La oss si vi bytter til 1kΩ (R20=1k, R21=1k).

• Termisk støy i 1kΩ er ca. 4 nV/√Hz.
• Nå blir totalstøyen ut fra bufferen betydelig lavere (redusert fra ca. 18-20 nV/√Hz i scenario 1 til ca. 6-7 nV/√Hz her).
• Men: Denne støyen skal ganges opp med TPA3255 sin gain (12x) og legges til TPA3255 sin egenstøy på 85 µV.
• Bufferns bidrag på utgangen (grovt estimert for audiobåndet 20kHz):
  • Scenario 1 (NE5532/10k): ~3 µV inn * 12 gain = 36 µV støybidrag.
  • Scenario 2 (OPA1612/1k): ~0.9 µV inn * 12 gain = 11 µV støybidrag.
• Total støy på utgang (kvadratisk summering med TPA3255s gulv på 85 µV):
  • Med NE5532: $\sqrt{85^2 + 36^2} \approx 92 \mu V$
  • Med OPA1612: $\sqrt{85^2 + 11^2} \approx 86 \mu V$
• Resultat: Total støy på utgangen reduseres fra ca. 92 µV til 86 µV. Dette er en målbar forbedring (ca. 0.6 dB lavere støy), men det er TPA3255 sin egenstøy som setter grensen.

Eksempel 3: Optimaliserte motstander og Gain på 12dB (4x)
Hvis du endrer R21 til 4kΩ og R20 til 1kΩ (Gain = -4 eller 12dB).

• Når du øker gain i bufferen, forsterker du inngangssignalet før det treffer TPA3255.
• Støyen ut av bufferen vil øke noe pga høyere forsterkning av inngangsstøy og motstandsstøy.
• Resultat: Selve støygulvet på utgangen av høyttaleren (når det er stille) vil faktisk kunne øke litt sammenlignet med eksempel 2, fordi bufferen nå sender ut mer støy som TPA3255 forsterker videre.
• Fordel: Hvis kilden din er svak, vil du få bedre Signal-til-Støy forhold (SNR) ved høyt volum, fordi signalet er sterkere i forhold til TPA3255 sin faste egenstøy på 85 µV. Men i ren tomgangsstøy (hissing i diskanten) vil dette alternativet være dårligere eller likt eksempel 2.

3. Vurdering av forvrengning (THD)

• NE5532: I følge THD_NE5532.png ligger forvrengningen (THD) typisk rundt 0.0004% til 0.001% ved 1 kHz (avhengig av last).
• 
  OPA1612: Databladet oppgir ekstremt lav forvrengning, ned mot 0.000015% ved 1 kHz.
  
  
  
• 
  TPA3255: I følge Figur 5 i tpa3255.pdf, ligger THD+N for selve forsterkeren rundt 0.005% - 0.01% ved 1 Watt (1 kHz, 4 Ohm).
  
  

Konklusjon om forvrengning:

Selv om OPA1612 har ekstremt mye lavere forvrengning enn NE5532 (en faktor på 10-100x bedre), er TPA3255 sin egenforvrengning ca. 10 ganger høyere enn det NE5532 presterer i dag.

Flaskehalsen for forvrengning er selve TPA3255-chippen og utgangsfilteret, ikke NE5532-bufferen. Å bytte til OPA1612 vil teoretisk sett gjøre signalet inn til TPA3255 renere, men du vil neppe kunne måle forskjell på høyttalerutgangen fordi TPA3255 sin egenforvrengning "maskerer" forbedringen.

Oppsummering
Du vil hente mest ved å bruke Eksempel 2 (OPA1612 med 1k/1k motstander), men gevinsten er begrenset av TPA3255 sine egne spesifikasjoner. Du kan forvente en reduksjon i totalt støygulv på under 1 dB, og ingen praktisk endring i total forvrengning.

Spoiler: Kimi

Analyse: Bytte fra NE5532 til OPA1612 i TPA3255EVM
Jeg har gått gjennom databladene for NE5532, OPA1612 og TPA3255 og gjort beregninger på støy og forvrengning. Her er resultatene.
Kretsforståelse
Opampen er koblet som inverterende forsterker med Rin = Rf = 10kΩ. Gain = -Rf/Rin = -10k/10k = -1 (0 dB). TPA3255 har gain på 21.5 dB (11.9x).
Forvrengning
Fra måledataene du delte ser vi at NE5532 med 10kΩ belastning har THD+N rundt 0.0004% ved 1kHz. OPA1612 har ifølge databladet 0.000015% ved samme frekvens. TPA3255 har 0.006% THD+N ved 1W.
Total forvrengning blir kvadratrtsummen: sqrt(opamp^2 + TPA3255^2)
Med NE5532: sqrt(0.0004%^2 + 0.006%^2) = 0.00601% Med OPA1612: sqrt(0.000015%^2 + 0.006%^2) = 0.00600%
Forvrengningsforbedring: 0.3% (0.03 dB) - praktisk ingen forskjell. TPA3255 dominerer fullstendig.
Støy - det viktige poenget
Her må vi skille mellom to tilfeller:
Tilfelle 1: Beholde 10kΩ motstander
NE5532: en = 5 nV/√Hz, termisk støy 10kΩ = 12.8 nV/√Hz, strømstøy ~1 pA/√Hz * 10kΩ = 10 nV/√Hz. Total: sqrt(5^2 + 12.8^2 + 10^2) = 17 nV/√Hz
OPA1612: en = 1.1 nV/√Hz, termisk støy 12.8 nV/√Hz, strømstøy 1.7 pA/√Hz * 10kΩ = 17 nV/√Hz. Total: sqrt(1.1^2 + 12.8^2 + 17^2) = 21.3 nV/√Hz
Med 10kΩ motstander blir OPA1612 faktisk STØYERE enn NE5532 pga høyere strømstøy!
Tilfelle 2: Optimaliserte motstander (1kΩ)
NE5532: sqrt(5^2 + 4.05^2 + 1^2) = 6.6 nV/√Hz OPA1612: sqrt(1.1^2 + 4.05^2 + 1.7^2) = 4.5 nV/√Hz
Her vinner OPA1612, men forskjellen er liten.
Total utgangsstøy fra TPA3255
TPA3255 egenstøy: 85 μV A-weighted
Med NE5532 10kΩ: opamp bidrar 28.6 μV → total 89.7 μV Med OPA1612 1kΩ: opamp bidrar 8.2 μV → total 85.4 μV
Støyforbedring: 4.8% (0.4 dB)
Konklusjon
Bytte til OPA1612 gir:

• Forvrengning: 0.03 dB forbedring (ubetydelig)
• Støy: 0.4 dB forbedring (bare med optimaliserte 1kΩ motstander)

Med originale 10kΩ motstander blir OPA1612 faktisk støyere pga høyere inngangsstrømstøy (1.7 vs ~1 pA/√Hz).
Anbefaling: Ikke verdt byttet med mindre du har andre krav (DC-presisjon, båndbredde, eller vil redusere motstandene betydelig).
Vil du ha med beregningene for gain = 12 dB også?

Spoiler: ChatGPT

1) Jeg forstår buffertrinnet og hvorfor gain = −1

I skjemaet ditt er hver NE5532 koblet som en inverterende forsterker rundt et “virtuelt jordpunkt” (VMID):

• + (ikke-inverterende) inngang ligger på VMID (bias midt i single-supply).
• Signalet kommer inn via Rin = 10 kΩ til − (inverterende) inngang.
• Tilbakekobling fra utgangen via Rf = 10 kΩ til samme −-node.

For en inverterende kobling er spenningsforsterkningen:


Gain = −Rf / Rin = −10k / 10k = −1


Minus-tegnet betyr at utgangen blir 180° faseinvertert i forhold til inngangen. VMID gjør at hele AC-signalet “svinger rundt” midtsupply (i stedet for rundt 0 V), slik at opampen kan jobbe på single-supply uten å klippe ved 0 V.


(De små kondensatorene over Rf i skjemaet er klassisk HF-kompensasjon/stabilitet, men de påvirker ikke DC/lydfrekvens gain-uttrykket over.)


2) Datablad-tallene vi faktisk får lov å bruke
NE5532 (støy)

• Inngangsstøyspenning (densitet) ved 1 kHz: 5 nV/√Hz
• Inngangsstøystrøm (densitet) ved 1 kHz: 0,7 pA/√Hz
  ne5532
  

OPA1612 (støy + forvrengning)

• Ved 1 kHz: en = 1,1 nV/√Hz og in = 1,7 pA/√Hz
  opa1612-q1
  
  
• Databladet forklarer også eksplisitt at lavest støy avhenger av kildeimpedans, og at OPA1612 er et godt valg når kildeimpedans < 1 kΩ
  opa1612-q1
  
  
• THD+N (G=+1, 1 kHz, 3 Vrms): 0,000015%
  opa1612-q1
  
  
• Databladet sier også THD+N er < 0,00008% gjennom audio-båndet (under oppgitte testbetingelser)
  opa1612-q1
  

TPA3255 (det som setter “gulvet”)

• Inngangsresistans RIN = 20 kΩ
• Inverterende spenningsgain G = 21,5 dB (≈ 11,9×)
• Utgangsstøy (integrert), A-veid, med inngangskondensator jordet: 85 µV
• THD+N ved 1 W: 0,006% (BTL tabellen)

3) Støy: hvorfor OPA1612 ikke automatisk gir lavere støy med 10k/10k

Den viktige datasheet-ideen er denne: total støy er RSS (root-sum-square) av bidrag fra:

• motstands-termisk støy
• opampens spenningsstøy (en)
• opampens strømstøy (in) som blir til spenning via resistansene

OPA1612-databladet viser samme logikk og gir støyoppsett for gain-koblinger.


I din inverterende −1-kobling er dette en veldig nyttig “ingeniør-tilnærming” (ikke en perfekt modell, men den viser mekanismen):

• “Effektiv” motstand i summenoden for termisk støy: Req = Rin || Rf
• “Noise gain” for inverterende: NG = 1 + Rf/Rin
• Opamp spenningsstøy forsterkes omtrent med NG
• Opamp strømstøy i inverterende inngang gir omtrent spenningstøy: in * Rf

Termisk støy som referanse

Termisk støy i en motstand: sqrt(4 k T R)


Ved romtemp gir dette omtrent:

• 10 kΩ: ca. 12,9 nV/√Hz
• 5 kΩ: ca. 9,1 nV/√Hz
• 1 kΩ: ca. 4,1 nV/√Hz
• 500 Ω: ca. 2,9 nV/√Hz

4) Tre konkrete eksempler (med delberegninger)

Jeg bruker:

• Audio-bånd ~ 20 kHz (for å integrere nV/√Hz til µV RMS). Dette er ikke identisk med A-vekting, men greit som “førsteordens” sammenlikning.
• TPA3255 gain = 21,5 dB (≈ 11,9×).
  tpa3255
  
  
• TPA3255 “gulv” = 85 µV A-veid utgangsstøy.
  tpa3255
  

Eksempel A — Samme som TI: 10k/10k, gain = −1 (NE5532 → OPA1612)

A1) NE5532 med 10k/10k

• Rin = Rf = 10k → Req = 5k
• NG = 1 + 10k/10k = 2
• Termisk nettverksstøy ≈ NG * sqrt(4kT*Req) = 2 * støy(5k) ≈ 2 * 9,1 = 18,2 nV/√Hz
• Opamp en-bidrag ≈ NG * en = 2 * 5 = 10 nV/√Hz
  ne5532
  
  
• Opamp in-bidrag ≈ in * Rf = 0,7 pA * 10k = 7 nV/√Hz
  ne5532
  
  
• RSS: sqrt(18,2² + 10² + 7²) ≈ 21,9 nV/√Hz

Integrert til ~20 kHz: 21,9 nV/√Hz * sqrt(20000) ≈ 3,1 µV RMS ved bufferutgang.
Gjennom TPA (11,9×): ≈ 37 µV RMS på høyttalerutgangen fra bufferstøy alene.
Total utgangsstøy ≈ sqrt(85² + 37²) µV ≈ 93 µV RMS.


A2) OPA1612 med 10k/10k (samme gain)

• Samme termisk nettverk: 18,2 nV/√Hz
• en-bidrag: 2 * 1,1 = 2,2 nV/√Hz
  opa1612-q1
  
  
• in-bidrag: 1,7 pA * 10k = 17 nV/√Hz
  opa1612-q1
  
  
• RSS: sqrt(18,2² + 2,2² + 17²) ≈ 25,0 nV/√Hz

→ buffer ~3,5 µV RMS → på utgang ~42 µV → total ≈ sqrt(85² + 42²) ≈ 95 µV.


Konklusjon for Eksempel A:
Med 10k/10k blir OPA1612 faktisk ikke en støygevinst her, fordi strømstøyen (in) ganger 10k blir stor. Databladet sier også nettopp at OPA1612 er “best” når kildeimpedans er lav (<1 kΩ).

opa1612-q1




Eksempel B — Optimaliserte motstandsverdier rundt OPA1612, samme gain = −1

Hvis målet er lavest mulig støy fra bufferen, må du ned med resistansene (slik at in*R blir liten og termisk støy går ned).


En praktisk “mellomting”:


OPA1612 med 2k/2k, gain = −1

• Req = 1k, NG = 2
• Termisk nettverk: 2 * støy(1k) ≈ 2 * 4,1 = 8,1 nV/√Hz
• en-bidrag: 2 * 1,1 = 2,2 nV/√Hz
  opa1612-q1
  
  
• in-bidrag: 1,7 pA * 2k = 3,4 nV/√Hz
  opa1612-q1
  
  
• RSS: sqrt(8,1² + 2,2² + 3,4²) ≈ 9,1 nV/√Hz

→ buffer ~1,3 µV RMS → på utgang ~15 µV → total ≈ sqrt(85² + 15²) ≈ 86 µV.


Hva betyr det i praksis på TPA3255-utgangen?
Sammenliknet med “TI/NE5532 10k/10k”-tilfellet (~93 µV), kommer du ned til ~86 µV: ca. 0,6 dB lavere.


Viktig tradeoff (fra skjemaet ditt):

• Inngangsimpedansen blir ~Rin (altså 2 kΩ i stedet for 10 kΩ).
• Inngangskondensatoren er 10 µF i skjemaet. Med 10 kΩ gir det lav høypass-knekk; med 2 kΩ flytter du knekket opp (du må typisk øke C tilsvarende hvis du vil beholde samme lave cutoff).

Eksempel C — Optimaliserte motstander og gain = 12 dB i buffertrinnet

12 dB betyr spenningsgain ≈ 4×. Med inverterende kobling betyr det:


Gain = −Rf / Rin = −4 → Rf = 4 * Rin
Noise gain blir NG = 1 + Rf/Rin = 5 (altså større støyforsterkning internt).


Hvis vi velger moderate verdier (for ikke ekstremt lav Rin):


OPA1612 med Rin = 1k, Rf = 4k (gain ≈ −12 dB / −4×)

• Req = 1k || 4k = 800 Ω
• NG = 5
• Termisk nettverk: 5 * støy(800 Ω) ≈ 5 * 3,6 = 18 nV/√Hz
• en-bidrag: 5 * 1,1 = 5,5 nV/√Hz
  opa1612-q1
  
  
• in-bidrag: 1,7 pA * 4k = 6,8 nV/√Hz
  opa1612-q1
  
  
• RSS ≈ sqrt(18² + 5,5² + 6,8²) ≈ 20 nV/√Hz

→ buffer ~2,8 µV RMS → på utgang ~34 µV → total ≈ sqrt(85² + 34²) ≈ 92 µV.


Tolkning:
Selv om du har “optimalisert” resistansene litt, så gjør høyere gain (via NG=5 og større Rf) at bufferens egenstøy igjen blir en betydelig bidragsyter. Resultatet blir omtrent tilbake i samme gate som originalen, ikke en stor forbedring.


Hvis du “maks-optimaliserer” for støy ved 12 dB må Rin enda lavere (for å holde Rf lav), men da blir:

• ekstremt lav inngangsimpedans
• inngangskondensatoren må opp mye for å ikke miste bass

5) Hvor mye lavere kan utgangsstøyen realistisk bli?

Med TPA3255-databladets 85 µV A-veide utgangsstøy som gulv

tpa3255

, kan du ikke komme dramatisk lavere på høyttalerutgangen bare ved å bytte bufferopamp.



Tallene over viser i praksis:

• “TI/NE5532 10k/10k”: ~93 µV
• “OPA1612 men fortsatt 10k/10k”: ~95 µV (altså litt dårligere)
• “OPA1612 og lavere motstander (2k/2k)”: ~86 µV

Så beste realistiske gevinst her er typisk rundt 0,6–0,7 dB, fordi TPA3255 sin egen utgangsstøy dominerer når bufferbidraget blir lite.


6) Forvrengning: hvor mye bedre blir det?

Her er forholdstallene (bare fra databladene og grafen din):

• TPA3255: 0,006% THD+N ved 1 W
  tpa3255
  
  
• OPA1612: 0,000015% THD+N ved 1 kHz, 3 Vrms (typisk test)
  opa1612-q1
  og <0,00008% over audiobåndet under oppgitte forhold
  opa1612-q1
  
  
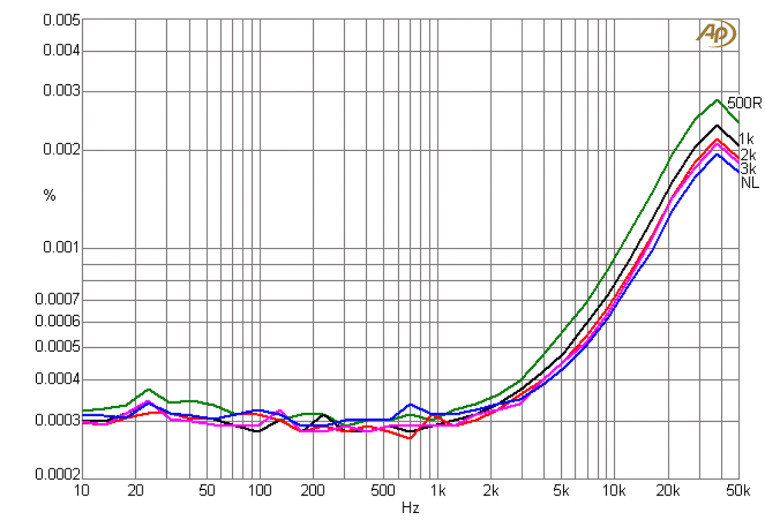
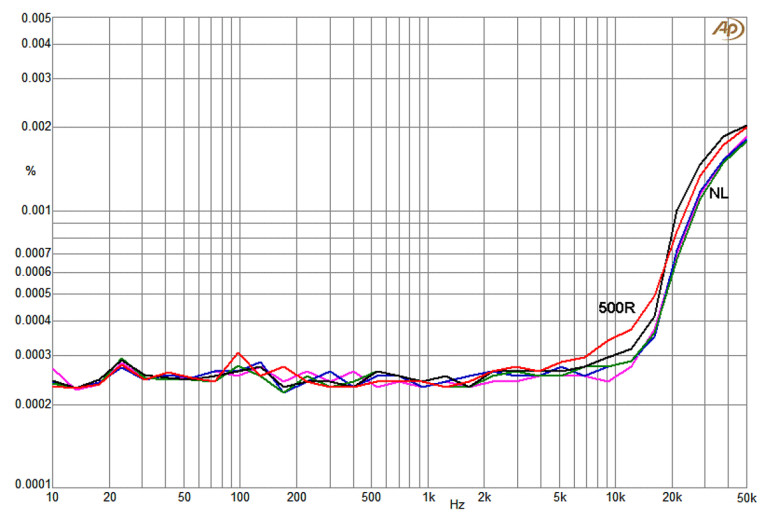
• NE5532: grafen du lastet opp viser typisk rundt noen 0,0003–0,0005% i midbånd (og øker i toppen) ved 9 Vrms og ulike laster.

Når du kaskaderer to trinn med THD:

• Den største (TPA3255) dominerer nesten alltid.
• Å gå fra “NE5532-nivå” til “OPA1612-nivå” i buffertrinnet flytter derfor system-THD svært lite så lenge buffertrinnet ikke klipper og ikke driver en urealistisk last.

Med andre ord: Byttet kan gi lavere forvrengning i buffertrinnet isolert, men den målbare forbedringen i total THD+N på høyttalerutgangen blir normalt neglisjerbar, fordi 0,006% (TPA3255 @1 W) er mange størrelsesordener større.

tpa3255




Bottom line (rett fram)

1. Gain = −1 fordi det er inverterende kobling med Rin=Rf og VMID som referanse.
2. Med 10k/10k får du ikke støygevinst av OPA1612; strømstøyen in gjennom 10k tar mye av “1,1 nV/√Hz”-fordelen.
3. Med lavere motstander (typisk i området der effektiv impedans er <1 kΩ) kan OPA1612 gi litt lavere total utgangsstøy, men gevinsten stopper fort fordi TPA3255 sitt 85 µV-gulv dominerer.
4. Forvrengning på systemnivå endres normalt svært lite; TPA3255 dominerer.

Hvis du vil, kan jeg ta samme regnestykke på A-veid basis (mer korrekt sammenlikning mot 85 µV-tallet), men da må du fortelle meg hvilket målebånd/filtre du vil anta for buffertrinnet (AES17/A-weight/20 kHz flat).

Den helt nye z.ai er utrolig bra

Spoiler: Z.ai

ANALYSE AV KRETSEN OG STOYBEREGNINGER
1. KRETSENFORKLARING - HVERFOR GAIN ER -1
Fra TPA3255EVM-skjemaet ser vi at opampen er konfigurert som en inverterende forsterker:

Signal in --> [10kΩ] --> Inverting input (-)
|
[10kΩ] |
| |
+---+--> Output
|
[Op-amp]
|
Non-inverting (+) --> VMID (virtual ground)

For en inverterende forsterker: Gain = -Rf / Rin = -10kΩ / 10kΩ = -1

Dette betyr at utgangen er invertert (180 grader faseforskyvet) men med samme amplitude som inngangen. TI bruker denne konfigurasjonen for å:

• Konvertere single-ended signal til differential signal (to faser)
• Matche impedans mot TPA3255's differentielle inngang
• Isolere kilde fra effektforsterkeren

2. STOYDATA FRA DATABLADENE

Parameter	NE5532	OPA1612-Q1
Spenningstoy (en) @ 1kHz	5 nV/√Hz	1.1 nV/√Hz
Stromtoy (in) @ 1kHz	0.7 pA/√Hz	1.7 pA/√Hz
THD+N @ 1kHz, 3Vrms	~0.001%	0.000015%

TPA3255 (fra datablad):

• Utgangsstoy (A-vektet, inngang jordet): 85 µV
• Spenningsgain: 21.5 dB = 11.89x
• THD+N @ 1W, 4Ω: 0.006%

3. STOYBEREGNINGER - GAIN = -1
For inverterende konfigurasjon med Rf = Rin = 10kΩ:

Nokkelprinsipp: For stoyanalyse er det "stoygain" som er relevant:

• Signal gain = -1
• Stoy gain = 1 + (Rf/Rin) = 2

Total inngangsreferer stoytetthet:

e_total = √(en² + (in × R_eq)² + 4kT × R_eq)

hvor R_eq = Rf || Rin = 5kΩ (parallellkobling)


NE5532:

• Termisk stoy fra 5kΩ: √(4 × 1.38×10^-23 × 300 × 5000) = 9.1 nV/√Hz
• Stromtoy-bidrag: 0.7pA × 5kΩ = 3.5 nV/√Hz
• Spenningstoy: 5 nV/√Hz

Total inngangsreferer: √(5² + 3.5² + 9.1²) = √(25 + 12.3 + 82.8) = 10.9 nV/√Hz


Utgangsstoy (med stoy gain = 2): 21.8 nV/√Hz


OPA1612:

• Termisk stoy fra 5kΩ: 9.1 nV/√Hz (samme)
• Stromtoy-bidrag: 1.7pA × 5kΩ = 8.5 nV/√Hz
• Spenningstoy: 1.1 nV/√Hz

Total inngangsreferer: √(1.1² + 8.5² + 9.1²) = √(1.2 + 72.3 + 82.8) = 12.5 nV/√Hz


Utgangsstoy (med stoy gain = 2): 25.0 nV/√Hz


Viktig observasjon: Med 10kΩ motstander dominerer termisk stoy fra motstandene! OPA1612s lavere spenningstoy gir ingen fordel fordi motstandsstoyen er høyere.


4. OPTIMALISERT KRETSEN MED LAVERE MOTSTANDSVERDIER
Du nevnte at du vil "utnytte OPA1612 best mulig". Dette betyr å redusere motstandene for a minimere termisk stoy.


La oss si du bruker Rf = Rin = 1kΩ istedenfor 10kΩ:


NE5532 med 1kΩ motstander (R_eq = 500Ω):

• Termisk stoy: √(4kT × 500) = 2.9 nV/√Hz
• Stromtoy-bidrag: 0.7pA × 500Ω = 0.35 nV/√Hz
• Spenningstoy: 5 nV/√Hz

Total: √(5² + 0.35² + 2.9²) = 5.8 nV/√Hz Utgangsstoy: 11.6 nV/√Hz


OPA1612 med 1kΩ motstander (R_eq = 500Ω):

• Termisk stoy: 2.9 nV/√Hz
• Stromtoy-bidrag: 1.7pA × 500Ω = 0.85 nV/√Hz
• Spenningstoy: 1.1 nV/√Hz

Total: √(1.1² + 0.85² + 2.9²) = 3.2 nV/√Hz Utgangsstoy: 6.4 nV/√Hz


Forbedring med OPA1612 vs NE5532 (begge med 1kΩ): Faktor: 11.6 / 6.4 = 1.81x lavere stoytetthet


5. TOTAL STOY VED TPA3255 UTGANGEN
TPA3255 har allerede en egen utgangsstoy på 85 µV (A-vektet). La oss beregne hvordan opamp-stoyen bidrar.


Integrert stoy over audio-bandet (20Hz-20kHz = 19980 Hz):


NE5532 (10kΩ motstander):

• Opamp utgangsstoy: 21.8 nV/√Hz × √19980 = 3.1 µVrms
• Forsterket av TPA3255 (gain 11.89x): 3.1 × 11.89 = 36.9 µVrms

OPA1612 (1kΩ motstander, optimalisert):

• Opamp utgangsstoy: 6.4 nV/√Hz × √19980 = 0.9 µVrms
• Forsterket av TPA3255: 0.9 × 11.89 = 10.7 µVrms

Total systemstoy ved TPA3255 utgang:


NE5532 (10kΩ): √(85² + 36.9²) = 92.6 µV OPA1612 (1kΩ): √(85² + 10.7²) = 85.7 µV


Forbedring: 92.6 / 85.7 = 1.08x (8% lavere total stoy)


Merk: TPA3255's egen stoy dominerer totalstoyen, saa opamp-stoyen har begrenset innvirkning.


6. BEREGNING MED GAIN = 12dB (GAIN = 4)
12dB = 20 × log10(G) → G = 4


For inverterende forsterker med gain = -4:

• Rf / Rin = 4
• Hvis Rin = 1kΩ, saa Rf = 4kΩ
• R_eq = Rf || Rin = 4kΩ || 1kΩ = 800Ω
• Stoy gain = 1 + 4 = 5

NE5532 (Rf=4kΩ, Rin=1kΩ):

• Termisk stoy (800Ω): 3.6 nV/√Hz
• Stromtoy-bidrag: 0.7pA × 800Ω = 0.56 nV/√Hz
• Spenningstoy: 5 nV/√Hz

Inngangsreferer: √(5² + 0.56² + 3.6²) = 6.2 nV/√Hz Utgangsstoy (stoy gain = 5): 31.0 nV/√Hz


OPA1612 (Rf=4kΩ, Rin=1kΩ):

• Termisk stoy: 3.6 nV/√Hz
• Stromtoy-bidrag: 1.7pA × 800Ω = 1.36 nV/√Hz
• Spenningstoy: 1.1 nV/√Hz

Inngangsreferer: √(1.1² + 1.36² + 3.6²) = 4.0 nV/√Hz Utgangsstoy (stoy gain = 5): 20.0 nV/√Hz


Forbedring med OPA1612 ved gain=4: 31.0 / 20.0 = 1.55x lavere stoytetthet


Ved TPA3255 utgang (men nå forsterkes opamp-stoyen også av gain=4):


NE5532: 31.0 nV/√Hz × √19980 × 11.89/4 = 52.2 µV (bidrag) OPA1612: 20.0 nV/√Hz × √19980 × 11.89/4 = 33.6 µV (bidrag)


Total systemstoy:

• NE5532: √(85² + 52.2²) = 99.7 µV
• OPA1612: √(85² + 33.6²) = 91.4 µV

Forbedring: 99.7 / 91.4 = 1.09x (9% lavere)


7. FORVRENGNINGSANALYSE
Fra databladene:

Komponent	THD+N @ 1kHz
NE5532 @ 9Vrms	~0.001% (fra graf)
OPA1612 @ 3Vrms	0.000015%
TPA3255 @ 1W, 4Ω	0.006%

TPA3255's forvrengning (0.006%) er ALLEREDE mye hoyere enn begge opampene. Dette betyr:

1. TPA3255 dominerer total forvrengning - opampens bidrag er neglisjerbart
2. Bytte fra NE5532 til OPA1612 vil ha minimal praktisk effekt på total forvrengning

Estimat av total THD+N:


Forvrengning legger seg ikke enkelt sammen, men hvis vi antar uavhengige kilder:


TPA3255 alene: 0.006% Med NE5532 (bidrag ~0.001% × gain): ~0.006% (ingen merkbarendring) Med OPA1612 (bidrag ~0.000015% × gain): ~0.006% (ingen merkbarendring)


8. KONKLUSJON

Scenario	Stoyforbedring	Forvrengningsforbedring
Samme motstander (10kΩ), G=-1	OPA1612 har HOYERE stoy	Neglisjerbar
Optimalisert (1kΩ), G=-1	1.81x lavere stoytetthet	Neglisjerbar
Optimalisert (1kΩ/4kΩ), G=-4	1.55x lavere stoytetthet	Neglisjerbar

Viktige punkter:

1. Stoy: Med hoye motstander (10kΩ) dominerer termisk motstandsstoy. OPA1612s fordel kommer forst frem ved lave motstandsverdier.
2. Total systemstoy: TPA3255's egen stoy (85 µV) dominerer. Opamp-bytte gir maksimalt 8-9% forbedring i total stoy.
3. Forvrengning: TPA3255's THD+N (0.006%) er 400 ganger hoyere enn OPA1612 (0.000015%). Opamp-bytte har ingen praktisk betydning for total forvrengning.
4. Anbefaling: Hvis du vil utnytte OPA1612 optimalt, bruk lave motstandsverdier (1kΩ eller mindre) for a minimere termisk stoy. Men forvent ikke dramatisk forbedring i total systemytelse fordi TPA3255 allerede setter begrensningen.

 

[Dalemark]

Dette var interesant. Resultater i testene til Douglas Self viser at opa NE5532 overall holder seg bra. Testen viser også forskjellige utslag på input impedanese og laster. Mitt tenkte bruksområde for TI3255EVM er basert på lav impedanse inn. Jeg vil også velge å se på forvrengning i frekvenser over 1k - 2k Hz, da ampen skal drive mellomtone og diskant.

Bufferet vi tidligere har simulert har et Voltage-follower kretsløp med motstand. Ved målinger basert på sammenligninger med NE5532 vil jeg utfra mine kriterier se nærmere på OPA2210.

Her er forvrengningen for de to.

NE5532

Figure 4: NE5532 voltage-follower with no-load (NL) plus 3kΩ, 2kΩ, 1kΩ, and 500Ω loads. Output 9Vrms; ±15V rails. Rs=40Ω.



OPA2210

Figure 29: OPA2210 voltage-follower with no-load (NL) plus 3kΩ, 2kΩ, 1kΩ, 500Ω loads. Output 9 Vrms ±15V rails.


Hvorvidt TI3255EVM bruker voltage-follower eller f.eks shunt feedback vet jeg ikke. Dersom ikke støyen er i pre og egenstøy gir utfordring, vil sannsynlig ikke opampen være kilde til dette når vi ser på støytallene i testen. Balansert inn i bufferkort vil da heller ikke påvirke støy da vi ikke kan kjøre balansert inputs X4 i 3255.

 

[Dalemark]

Denne har 4 kanaler, balansert inn.

TPA3255 4-channel module review - $12.50 per channel but is it any good?

We see a lot of 2-channel TPA3255 based modules, but 4 channel ones are rarer. I bought this one off AliExpress for $50 including shipping - that's $12.50 per channel! Build quality is OK but not great. The power and speaker I/O is all screw terminals, where better modules use spades. The...

www.audiosciencereview.com

Målinger:

 

[Armand]

Hvorvidt TI3255EVM bruker voltage-follower eller f.eks shunt feedback vet jeg ikke.

Her ser du hvordan TPA3255EVM er koblet. Du ser at dette er som figur a, og dermed det han kaller shunt feedback.
Inngangsimpedansen blir da lik motstanden R1 i figur a. På TPA3255EVM er imput impedansen dermed 10k (R20)

I slike koblinger kan man ikke bare senke motstanden ned til f.eks 1k uten at man har kontroll på at kilden kan levere nok strøm.

Testen viser også forskjellige utslag på input impedanse

Ja, så hvis man vet at kilden har høy impedanse så blir valg av opamp viktig. I ditt tilfelle der utgangsimpedansen til kilden er 100 Ohm eller lavere spiller det ingen rolle.

Testen viser også forskjellige utslag på laster

Ja, så hvis man vet at lasten man skal drive er tung, må man velge opamp som er tilpasset dette..
I ditt tilfelle der lasten er 20k (TPA3255) så spiller det ingen rolle

Jeg vil også velge å se på forvrengning i frekvenser over 1k - 2k Hz, da ampen skal drive mellomtone og diskant.

Ja, det er viktig. Men matematikken er dessverre ikke på din side på noen måte
Du vil se at med lav impedanse på input og høy impedanse på utgangen så vil alle opamper som er tilpasset audio være massivt mye bedre enn TPA3255 med god margin. Se på grafen til TPA3255 modulen:

Den har 0,1% forvrengning ved 10kHz. Å senke bufferet fra 0,0008% til 0,0001% er bare tull. Total forvrengning vil synke fra 0,1000032% til 0,10000005%.
Det vil være nærmest umulig å måle, og i hvert fall umulig å høre forskjell på.
Til og med en opamp med 0,01% ville være mer enn god nok.

Du har egentlig en svært enkel problemstilling. Du har et kraftig lydkort med utgangsimpedans på 100 Ohm som kan drive inngangen til opampbufferet ditt, og du bufferet ditt skal drive en svært lett last på TPA3255 (20k).

Du burde egentlig bare koble deg utenom hele NE5532 og drive TPA3255 direkte.

Ved målinger basert på sammenligninger med NE5532 vil jeg utfra mine kriterier se nærmere på OPA2210

Som vist over er det - i denne applikasjonen - virkelig ikke noen vits.

Balansert inn i bufferkort vil da heller ikke påvirke støy da vi ikke kan kjøre balansert inputs X4 i 3255.

Du kunne jo laget deg et buffer med 4x balansert input og 4x SE output. Du ville da få fordelene balansert signaloverføring har i forhold til jordproblemer.
Men vær klar over at alle balanserte kretsløp har mer støy enn SE kretsløp.Rett og slett fordi det er flere komponenter involvert. Man kommer ikke unna det.

En praktisk test som er rask å gjøre og som kanskje kan få deg til å forstå dette bedre er følgende:
* Kortslutt inngangene (Lask til GND med kort kabel) til TPA3255 etter NE5532. Dette er null støy. Hør hva som kommer ut på høyttalerne dine da.
* Ta så bort denne kortslutningen og kortslutt inngangen til NE5532 i stedet. Da vil støyen fra denne gå inn på forsterkeren og du kan høre om det blir forskjell.

 

[Armand]

Denne har 4 kanaler, balansert inn.

TPA3255 4-channel module review - $12.50 per channel but is it any good?

We see a lot of 2-channel TPA3255 based modules, but 4 channel ones are rarer. I bought this one off AliExpress for $50 including shipping - that's $12.50 per channel! Build quality is OK but not great. The power and speaker I/O is all screw terminals, where better modules use spades. The...

www.audiosciencereview.com

Målinger:
Vis vedlegget 1179782

La oss analysere denne THD+N grafen. Man kan dele denne grafen opp i tre deler. Blått område er 100% støy (N), Gult område er en kombinasjon av støy og forvrengning(THD+N). Rødt område er kun forvrengning (THD).

Hvorfor er det slik?

Spoiler: Trykk her for et lettfattelig AI-svar

1. Blått område: "Støyen vinner over signalet"
Tenk deg at du sitter i et rom der et kjøleskap durer svakt i bakgrunnen. Denne duren er konstant (dette er støygulvet i forsterkeren).

• Helt til venstre: Hvis du hvisker veldig lavt, er kjøleskapsduren nesten like høy som stemmen din. Da er "feilprosenten" (støyen) veldig høy i forhold til signalet.
• Mot høyre i blå boks: Når du begynner å snakke høyere, er kjøleskapsduren fortsatt like lav, men stemmen din blir sterkere.
• Resultat: Støyen utgjør en stadig mindre prosentandel av totalen. Derfor stuper kurven nedover. Jo høyere effekt (lyd), desto mindre betyr den konstante bakgrunnsstøyen.

2. Gult område: "Sweet spot"
Her er signalet blitt så sterkt at vi ikke lenger bryr oss om bakgrunnsstøyen (kjøleskapet er "borte"). Samtidig jobber forsterkeren fortsatt innenfor komfortsonen sin.

• Her er det en balanse. Støyen er ubetydelig, og elektronikken har ennå ikke begynt å slite.
• Kurven flater ut fordi forsterkeren begynner å legge til litt egenfarging (forvrengning), men det holder seg stabilt lavt. Dette er området der forsterkeren låter renest.

3. Rødt område: "Veggen" (Clipping)
Her skjer det noe drastisk. Forsterkeren har en maksimal grense for hvor mye strøm og spenning den kan levere (forsyningsspenningen).

• Når kurven skyter rett til værs, er det fordi forsterkeren "treffer taket". Den prøver å lage lyden større enn den har plass til.
• Bølgetoppene i musikken blir kuttet flate (dette kalles clipping).
• Når en lydbølge blir kuttet flat, eksploderer forvrengningen fra f.eks. 0,005% til 1% og 10% på et øyeblikk. Det er dette som skjer i den bratte stigningen.

Kort oppsummert:

1. Blått: Signalet er for svakt til å overdøve suset.
2. Gult: Signalet er sterkt og rent.
3. Rødt: Signalet er for sterkt for forsterkeren, og lyden "knuser".

Siden vi vet at støyen dominerer ved 1W effekt, og vi vet at lasten er 4,7 Ohm kan vi regne ut signalspenningen.

Siden vi vet at N er 0,01% av signalet kan vi finne støyspenningen

Det er altså 217uV.

Det er ikke spesielt bra med tanke på at TPA3255 har en egenstøy på 85uV. Om det er det balanserte trinnet som støyer, eller om det er noe annet som støyer er ikke godt å si

 

[Dalemark]

TPA3255 4CH er ikke aktuell for det formålet jeg skal bruke dette til. Kanskje i en annen sammenheng.

En praktisk test som er rask å gjøre og som kanskje kan få deg til å forstå dette bedre er følgende:
* Kortslutt inngangene (Lask til GND med kort kabel) til TPA3255 etter NE5532. Dette er null støy. Hør hva som kommer ut på høyttalerne dine da.
* Ta så bort denne kortslutningen og kortslutt inngangen til NE5532 i stedet. Da vil støyen fra denne gå inn på forsterkeren og du kan høre om det blir forskjell.

Det er nettopp testens bevis på hvor lave støytall opamp opererer med jeg sikter til her. Se sitat under:

Dersom ikke støyen er i pre og egenstøy gir utfordring, vil sannsynlig ikke opampen være kilde til dette når vi ser på støytallene i testen

Hvilke fordel vil bypass av NE5532 gi?

 

[Armand]

Hvilke fordel vil bypass av NE5532 gi?

I praksis: Ingen.
Og nettopp derfor lurer jeg på hvorfor du vil lage noe buffer i det hele tatt. Hva er poenget?

EDIT:
Du har jo sagt at poenget er å få lavere støy, og vil se om et buffer gjør situasjonen bedre. Ved å gjøre denne enkle testen så vil du selv erfare at det ikke er NE5532 som er problemet. Du kan til og med simulere verdens beste buffer ved å koble alle ingangene til GND. Det går ikke an å slå dette.

Kan du teste dette?