Matte, gåter og vitenskap Mattenøtter. Hjelp... Eller utfordring?

[Yelll]

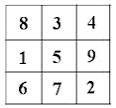
En tallrekke, fra 1 til 9. Alle tallene kan brukes bare en gang.



X X X
+ X X X
-----------
= X X X

Dvs at alle tallene skal være representert, 1 gang. Og svaret skal være riktig.


Hjelp? Please...



Mvh matterookie...





Edit erato... Du har rett... De skal rett over hverandre.. Feil rettet.

 

[erato]

Er posisjonene rett her? Dvs

X X X
+ X X X
-----------
= X X X


eller skal den første Xen stå over + tegnet osv?

 

[Yelll]

Neida... De skal rett over hverandre. Sikkert enkelt, legge sammen... Men jeg kommer tilkort, med å bruke opp alle tallene i rekka 1-9, bare en gang...


Takk for korr Erato!


Mvh Yelll

 

[Pink_Panther]

128
+439
=567

 

[erato]

eller 134 + 658 = 792

 

[Yelll]

???????????????????????? og takk!


-y

 

[Pink_Panther]

Spørsmålstegn?? Lov å "ha en i mente" i denne oppgaven. Summen av to siffer kan godt være større enn 10.

 

[Slubbert]

Virker mer som et programmeringsproblem enn en mattenøtt. Finner lett noen løsninger, men da gjennom å teste mange permutasjoner. Ser ikke noen mer elegant matematisk løsning sånn rett frem i hvert fall.

124
+659
=783


125
+739
=864

357
+462
=819

Det finnes trolig et stort antall løsninger, men antall permutasjoner kan begrenses feks ved å utelukke A>500 && B>500 (hvis A+B=C), og sikkert mer til. Å utelukke unødvendige permutasjoner er dog et programmeringsproblem og ikke et matteproblem i tradisjonell forstand.

 

[Yelll]

Suverent! Takk!

 

[Slubbert]

Et svar på en mattenøtt ikke verdt så mye uten en løsningsmetode. Virker som tverrsummen av svaret alltid blir 18, ellers ser jeg ikke noen måte å løse dette enkelt på. Usikker på om det finnes noen, siden det er mange mulige svar.

 

[erato]

Det er flere ukjente enn sammenhenger her så det vil vel være mange løsninger ja.

 

[Proffen]

Kan ta en annen variant;
Du får utlevert følgende kort: konge, dame, knekt, ti, ni, åtte, syv, seks, fem
der kortene har verdiene vi er vant til.
Plasser så kortene slik at de danner et kvadrat, dvs tre*tre rekker.
Så skal summen i hver vertikale, horisontale og diagonale rekke bli den samme.
Hvordan resonnerer du deg frem til løsningen?
Hvordan blir kortene liggende?

mvh
Proffen

 

[Ulf-B]

Kan ta en annen variant;
Du får utlevert følgende kort: konge, dame, knekt, ti, ni, åtte, syv, seks, fem
der kortene har verdiene vi er vant til.
Plasser så kortene slik at de danner et kvadrat, dvs tre*tre rekker.
Så skal summen i hver vertikale, horisontale og diagonale rekke bli den samme.
Hvordan resonnerer du deg frem til løsningen?
Hvordan blir kortene liggende?

mvh
Proffen

Blir ikke dette en variant av den klassiske 1-9-magisk-kvadrat-varianten?



I stedet for 1-9 setter vi inn 5-13 - altså at vi øker alle tallene i figuren med 4?

Resonnementet er at summene vannrett, loddrett og diagonalt blir 15 i 1-9-kvadratet - og dermed 15+4+4+4 = 27 i ditt eksempel.

 

[Slubbert]

Denne var litt tricky. Finn X.

 

[Trondmeg]

Den vil jeg se på når jeg jeg finner frem blyant og papir. Har en ide om løsning.

 

[Larson]

løsningen ligger vel i å lage rettvinklete trekanter, med høyde a, hvorpå den korresponderende har høyde (x-a), og b med (x-b) og bruke pytagoras.

eksempel:
rundt a:
17^2 = a^2 + (x-b)^2
20^2 = a^2 + b^2

rundt b:
20^2 = b^2 + a^2
13^2 = b^2 + (x-a)^2


2 av likningene over er identiske.

uansett ender vi opp med 3 ulike likninger og 3 ukjente. løs mot x.

 

[Trondmeg]

prøv å løse dem da

 

[Larson]

Den er løst.

vi løser ut likningene og får:
x = +/- 3 * sqrt(41)
x = +/- sqrt(89)

siden x ikke kan være negativ strykes de negative resultatene og vi ender opp med 2 løsninger..

 

[Slubbert]

Det går an å redusere den til to likninger med to ukjente vha cosinussetningen. 3*sqrt(41) er riktig, sqrt(89) er ikke riktig, da blir a eller b negativ.

Én til:

 

[Trondmeg]

Da er du flinkere enn meg til å løse ligningene. Jeg brukte samme utgangspunkt, men hadde ikke tålmodighet med ligningene jeg endte opp med ......

 

[Larson]

https://www.wolframalpha.com/input/?i=17^2+=+a^2+++(x-b)^2;+20^2+=+a^2+++b^2;+13^2+=+b^2+++(x-a)^2

Her er ikke a eller b negativ ved sqrt(89), slubbert. Så det må være en annen grunn for at den ikke er gyldig som løsning.

 

[Slubbert]

Da er ikke likningssettet kompett. Det er også gitt av figuren at X ikke kan være litt over ni, siden punktet da ville havnet utenfor firkanten. Hvis du kaller punktet trekantene møtes for P og skriver det som Px, Py (x-verdi og y-verdi, gitt at nederste venstre hjørnet i firkanten er origo), så blir det:

1. (X-Py)^2+Px^2=17^2
2. (X-Px)^2+Py^2=13^2
3. (X-Px)^2+(X-Py)^2=20^2

Den har bare én gyldig løsning. Men det er ganske håpløst å nøste opp for hånd, så tolikningsløsningen er bedre.

 

[Slubbert]

Den her er fortsatt up for grabs.