HFS-labyrinten

[Ulf-B]

Vi snakker om en by. Og som Vintage Silver Pioneer har vært inne på: en russisk by. Men dagens Russland er jo ikke så gammelt, da.....

 

[Vintage Silver Pioneer]

Før eller etter kommunismens fall ?

 

[Vintage Silver Pioneer]

Skal vi til 2. verdenskrig ?

 

[Ulf-B]

Det som skjedde under 2. verdenskrig var avgjørende - både for byen, og for at det umlige ble mulig.

 

[Vintage Silver Pioneer]

7 statsledere kanskje.

 

[Vintage Silver Pioneer]

Stalingrad kanskje - senere Volgograv

 

[Steinar_Lund]

Jeg tenkte på at "nye eiere" kunne henvise til et land som etter Sovjetunionen hadde blitt en egen, uavhengig stat, men slik er det øyensynlig ikke.

Nå tenker jeg litt på St. Petersburg, ex Leningrad, men om de andre ledetrådene passer inn, vet jeg ikke.

 

[Ulf-B]

Vintage Silver Pioneer: Nei. Ingen assoisiasjoner til statsledere. Det umulige jeg tenker på, er noe så hverdagslig som en spasertur.

Steinar_Lund: Russland har bare overtatt eierskapet etter Sovjetunionen. Kortene ble imidlertid lagt i forbindelse med avslutningen av 2. verdenskrig. Som så mange andre kort.

 

[Vintage Silver Pioneer]

Disse spaserturene som gikk fra 7 til 5, er det en rundtur i den byen vi skal til ?

 

[Steinar_Lund]

Vintage Silver Pioneer: Nei. Ingen assoisiasjoner til statsledere. Det umulige jeg tenker på, er noe så hverdagslig som en spasertur.

Steinar_Lund: Russland har bare overtatt eierskapet etter Sovjetunionen. Kortene ble imidlertid lagt i forbindelse med avslutningen av 2. verdenskrig. Som så mange andre kort.

Da kommer jeg nok til kort.

 

[Ulf-B]

Vintage Silver Pioneer: Spaserturen jeg tenker på, er en helt spesiell rundtur i byen, ja...

Men etter 2. verdenskrig er ikke akkurat DEN spaserturen lenger mulig. Hvilket gjør det mulig å realisere den opprinnelige spaserturens utfordring.

 

[Vintage Silver Pioneer]

7 parker ?

 

[Ulf-B]

Nei - 7 av noe mye mer vanlig. Finnes "overalt".

 

[Vintage Silver Pioneer]

Kirker ?

 

[aam01]

Broer?

 

[Ulf-B]

Ikke Berlin. Vi skal til en by som ligger i Russland.

Opprinnelig med sju av ett eller annet, og en sveitser beviste at akkurat disse sju representerte en umulig ufordring. Idag er det bare fem igjen - og da er det ingen utfordring lenger.

 

[Vintage Silver Pioneer]

Tenkte også på broer , og på statuer

 

[Ulf-B]

Lurere å tenke på broer.

 

[Vintage Silver Pioneer]

St. Petersburg er jo kjent for sine mange broer.

 

[Ulf-B]

Ja - men det er ikke dit vi skal. I de gode gamle dager - før byen ble sovjetisk og russisk - representerte noen broer i byen en umulig utfordring.

 

[Vintage Silver Pioneer]

Budapest fikk jo alle broene ødelagt under 2.verdenskrig, men da er vi jo i Ungarn.

 

[Ulf-B]

Mange byer som ble ødelagt under 2. verdenskrig. Denne byen også. Og gjenoppbyggingen har ikke akkurat bevart mye av det gamle - snarere tvert i mot. Kan hende var det ikke så mye å bevare - hva vet vel jeg. Men vi skal altså til en russisk by - la det ikke være noen tvil om den saken.

 

[aam01]

Jeg tror vi skal til Kaliningrad, men jeg har problem med å si hvorfor.

 

[joha]

Kaliningrad. Koenigsbergbroene?
Sveitseren er Leonhard Euler.

Edit: ser aam01 svarte først, så passer ny oppgave til han.

 

[aam01]

Leonhard Euler, matematiker og han som beskrev problemet "Broene i Kønigsberg".

 

[Ulf-B]

Da var vi der! Vi skal til byen Kaliningrad – tidligere Königsberg – som ligger i den russiske enklaven mellom Polen og Litauen.

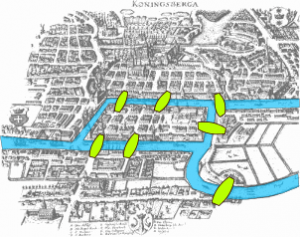
Da byen het Königsberg var det sju broer over elven Pregel (russisk Pregolye) som renner gjennom byen, i tilknytning til den lille øya sentralt i byen – og diskusjonen gikk om hvorvidt det var mulig å legge opp en rute, med fritt valgt startpunkt, slik at man gikk over samtlige broer, men bare én gang over hver bro:



Den sveitsiske matematikeren Leonhard Euler beviste i 1736 en gang for alle at det ikke ville være mulig. Med mindre man tyr til jukseløsningen som innebærer en lang ferd rundt utspringet til elven som renner gjennom byen. Eulers tanker var første skritt på veien mot moderne matematisk grafteori .

Etter den 2. verdenskrig kom Königsberg under Sovjetunionen (og senere Russland) – og fikk navnet Kaliningrad etter den sovjetiske presidenten Kalinin. I forbindelse med gjenoppbyggingen etter krigen, ble de sju broene redusert til fem – og hadde dette vært i de gode gamle dager, ville ikke Euler ha kommet på banen – for med dagens fem broer er det en smal sak å komme seg over alle broene på foreskreven måte:

 

[Vintage Silver Pioneer]

Pokker- akkurat litt sent ute

 

[aam01]

Vi skal til en hyggelig by i det sørlige Europa som tidligere var et fystedømme tilhørende en senere norsk konge.

 

[Steinar_Lund]

Sørlige Europa. Ikke nødvendigvis ved Middelhavskysten? Og senere norsk konge. Han var kanskje hverken norsk eller konge sånn til å begynne med?

 

[aam01]

Alle søreuropeiske byer ligger ikke ved kysten og flere norske konger var ikke norske i utgangspunktet.

 

[Steinar_Lund]

Nettopp. Da skal vi kanskje ikke så mange århundrer tilbake i tid?

 

[aam01]

Nei, det stemmer. Vi skal ikke tilbake til vikingene.

 

[oct]

Vi skal til en hyggelig by i det sørlige Europa som tidligere var et fystedømme tilhørende en senere norsk konge.

En fyrste fra dette fyrstedømmet ble senere norsk konge???.


mvh

 

[Steinar_Lund]

Tok denne senere kongen veien om Danmark? Eller Sverige?

 

[aam01]

Vi skal til en hyggelig by i det sørlige Europa som tidligere var et fystedømme tilhørende en senere norsk konge.

En fyrste fra dette fyrstedømmet ble senere norsk konge???.


mvh

Han var ikke fra dette fyrstedømmet, men han var fyste der og ble senere norsk konge.

 

[Steinar_Lund]

Haakon VII?

 

[aam01]

Tok denne senere kongen veien om Danmark? Eller Sverige?

Via Sverige.

 

[Ulf-B]

Karl Johan.

 

[aam01]

Karl Johan.

Greit nok med Karl Johan, men det er byen vi skal frem til.

 

[Ulf-B]

Karl Johan.

Greit nok med Karl Johan, men det er byen vi skal frem til.

Vi tar ett skritt ad gangen....